ЗАСТОСУВАННЯ МЕТОДІВ МАТЕМАТИЧНОГО АНАЛІЗУ ДЛЯ ДОВЕДЕННЯ ОЛІМПІАДНИХ НЕРІВНОСТЕЙ

Микола Вікторович Гаєвський; Людмила Володимирівна Ізюмченко; Інна Геннадіївна Ключник

doi:10.36550/2415-7988-2020-1-191-58-61

Микола Вікторович Гаєвський Центральноукраїнський державний педагогічний університет імені Володимира Винниченка https://orcid.org/0000-0001-5268-748X
Людмила Володимирівна Ізюмченко Центральноукраїнський державний педагогічний університет імені Володимира Винниченка https://orcid.org/0000-0001-8656-2220
Інна Геннадіївна Ключник Центральноукраїнський державний педагогічний університет імені Володимира Винниченка https://orcid.org/0000-0001-6874-7811

DOI: https://doi.org/10.36550/2415-7988-2020-1-191-58-61

Ключові слова: олімпіадні задачі, нерівності, похідна, дотична, точка перегину, n-1 рівних значення

Анотація

Нерівності займають важливе місце в математиці, зустрічаються у всіх розділах математики і мають безліч різних застосувань. Доведення нерівностей справляє значний вплив на формування та розвиток творчого мислення та творчої особистості учня в силу наявності різних способів доведення для нерівності. В статті досліджуються особливості підготовки учнів методам доведення конкурсних та олімпіадних нерівностей, в яких міститься величина виду 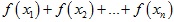із фіксованою сумою змінних 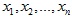. Розглянуто особливості використання апарату диференціального числення на рівні школяра старшої школи. Проаналізовано можливості доведення нерівностей з використання дотичної чи твердження n-1 рівних значень, розглянуто їх переваги та недоліки. За допомогою даних понять можна алгоритмізувати процес доведення деяких типів нерівностей. Для деяких задач наведено різні способи доведення, дані методи розв’язування нерівностей вимагають від учнів знання основ диференціального числення.

Посилання

Київські міські математичні олімпіади. 2003–2011 роки /А.В. Анікушин та ін. за ред. Б.В.Рубльова. Харків: Гімназія, 2011. 192с.

Вороний О.М. Готуємось до олімпіади з математики. Харків: Вид. група «Основа», 2008. 255 с.

Математичні олімпіади школярів України: 2001-2006. / Лейфура В.М., Мітельман І.М., Радченко В.М., Ясінський В.А. Львів: Каменяр, 2008. 348 с. / URL: https://www.twirpx.com/file/2049208/ (дата звернення 20.05.2020)

Ясінський В.А., Панасенко О.Б. Секрети підготовки школярів до Всеукраїнських та міжнародних олімпіад. Алгебра. Навчально-методичний посібник. Вінниця: Середняк Т.К., 2015. 272 с.

Ясінський В.А. Задачі математичних олімпіад та методи їх розв’язування. Тернопіль: Навчальна книга, Богдан, 2008. 208 с.

Сарана О.О. Математичні олімпіади: просте і складне поруч: Навч. посібн. Тернопіль: Навчальна книга. Богдан, 2011. 400 с.

Федак І.В. Методи розв’язування олімпіадних завдань з математики і не тільки їх. Чернівці.: Зелена Буковина. 2002. 340 с.

Харди Г.Г., Литлвуд Дж.Е., Пойа Г. Неравенства. М.: ИЛ, 1948. 458 с.

Беккенбах Э., Беллман Р. Неравенства. М.: Мир, 1965. 276 с.

Evan Chen. A Brief Introduction to Olympiad Inequalities. URL: https://web.evanchen.cc/handouts/Ineq/en.pdf (дата звернення 20.05.2020)